Hybrid Logical Clocks
PWLMtl 2019-10-03

Title dissection
What is a snapshot?
What makes a snapshot consistent?
Snapshots
Recording the global state of a distributed system is important, but not easy.
There's no globally shared memory or clock, and messages between nodes can be lost, delayed and reordered
A famous example of a snapshotting algorithm is Chandy-Lamport '85
Snapshots
Classic example of why distributed snapshots are necessary:
Bank accounts \(A\) and \(B\) are on separate computers.
Each has a balance of \($500\).
\(A\) reduces its balance by \($100\),
then transfers \($100\) to \(B\)
What is the state of this system at any point in time? Simply reading the balances of each account separately may show money as missing
Snapshots
Imagine a system comprised of nodes with unidirectional FIFO channels between them
A global state is consistent if it satisfies two conditions:
- \(send(m_{ij}) \in S_i \implies \\ m_{ij} \in C_{ij} \;XOR\; recv(m_{ij}) \in S_j\)
- \(send(m_{ij}) \notin S_i \implies \\ m_{ij} \notin C_{ij} \land recv(m_{ij}) \notin S_j\)
Snapshots
In plain words, at the time of the snapshot:
- If node \(i\) sent a message to node \(j\), the message is either in the channel between \(i\) and \(j\), or it has arrived at \(j\)
- If node \(i\) did not send a message to node \(j\), the message is neither in the channel between \(i\) and \(j\) nor at \(j\)
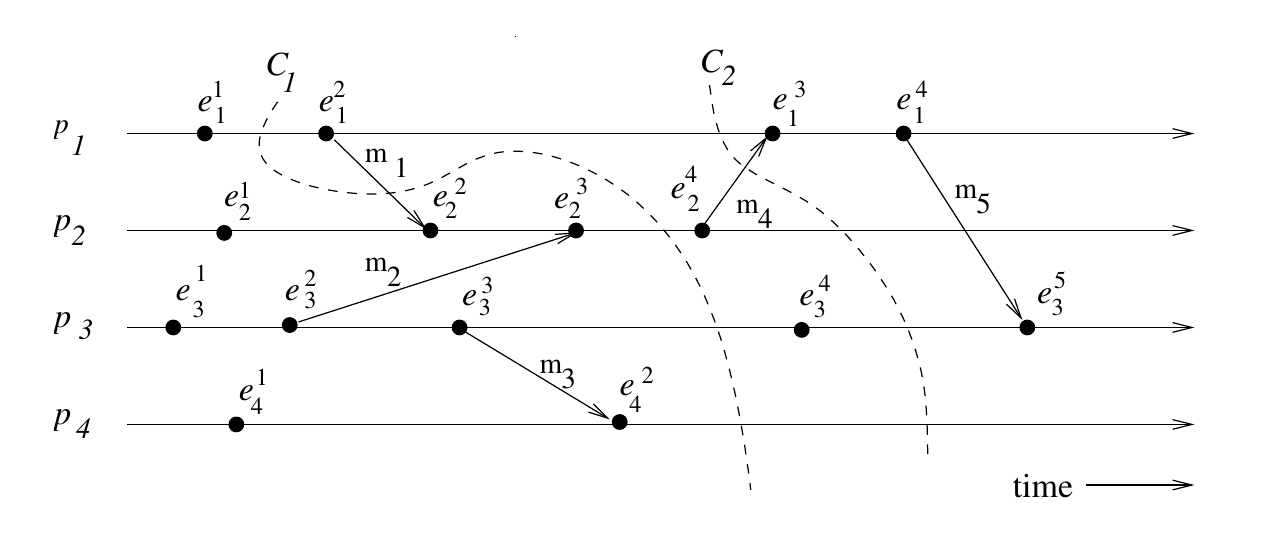
\(C_1\) is inconsistent, \(C_2\) is consistent
An introduction to
physical and logical time...

Physical time, as understood by a computer:
$ while true; do date +%s; sleep 1; done
1544033465
1544033466
1544033467
1544033468
1544033469
1544033470
1544033471
Problem: Drift
$ date
Fri Dec 7 10:00:00 EST 2018
[2 minutes later...]
$ date
Fri Dec 7 10:17:35 EST 2018
NTP (Network Time Protocol)

Congratulations! You've replaced your drifting clock with a connectivity requirement
Logical time
How do we order events without using physical time?
Rephrased: Can we define some relation \(hb\) that partially orders events?
Lamport Timestamps
- Proposed in 1978
- Nodes learn about time through the passing of information
Lamport Timestamps
- Node A receives \[(5, \text{Fall of the Roman Empire})\]
- Node A increments its clock \[LC = 6\]
- Node A replies \[(6, \text{Woodstock})\]
- Both nodes know Rome fell before Woodstock
Lamport Timestamps
Lamport timestamps find some consistent snapshots, but not all of them.
Vector Clocks
- Proposed in 1988
- Vectorized version of LC
- Each node maintains a vector of what it knows about the LCs at other nodes
- Vector clocks get updated when nodes send/receive messages to/from other nodes
- Vector clocks are compared in a pointwise fashion
- Vector clocks find all consistent snapshots
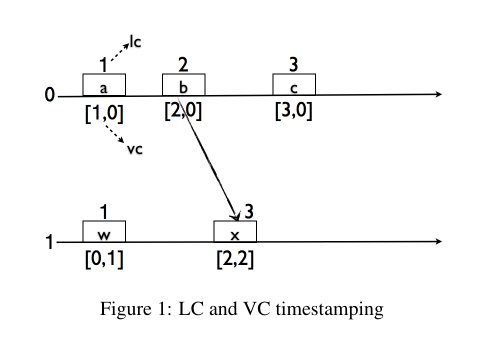
LC: (a, w)
VC: (a, w), (b, w), (c, w)
Vector Clocks work quite well, but without additional help, they O(N) space, where N is the number of nodes that ever existed your system, unless you have a means of generating and reusing globally unique names.
Vector Clocks are the base on which many alternative logical clocks build upon.
E.g: Dotted Version Vectors, Interval Tree Clocks, etc...
TrueTime
- Developed for Google's Spanner database
- Uses GPS and atomic clocks
- Will wait out uncertainty periods in order to avoid inconsistent snapshots
Assumptions that Simplify
(why I love this paper)
Find an element in a list: \(O(N)\)
Simplification:
Find an element in a sorted list: \(O(\log(N))\)
Simplifying assumptions
(why I love this paper)
Have a logical clock that finds all consistent snapshots: \(O(N)\)
Simplification
Have a logical clock that finds all consistent snapshots in a cluster of servers who occasionally synchronize their physical clocks: \(O(1)\)
Hybrid Logical Clocks — Problem Statement
Given a distributed system, assign each event \(e\) a timestamp \(l.e\) such that:
- \(e\) "happened before" (aka \(hb\)) \(f \implies l.e \lt l.f\)
- \(l.e\) can be represented with \(O(1)\) integers
- \(l.e\) is represented with bounded space
- \(l.e\) is "close to" \(pt.e\), i.e. \(|l.e - pt.e|\) is bounded
Naive implementation

Hybrid Logical Clocks — Problem Statement
Given a distributed system, assign each event \(e\) a timestamp \(l.e\) such that:
- \(e\) "happened before" (aka \(hb\)) \(f \implies l.e \lt l.f\) ✔
- \(l.e\) can be represented with \(O(1)\) integers ✔
- \(l.e\) is represented with bounded space ✔
- \(l.e\) is "close to" \(pt.e\), i.e. \(|l.e - pt.e|\) is bounded ❌
Counter-example
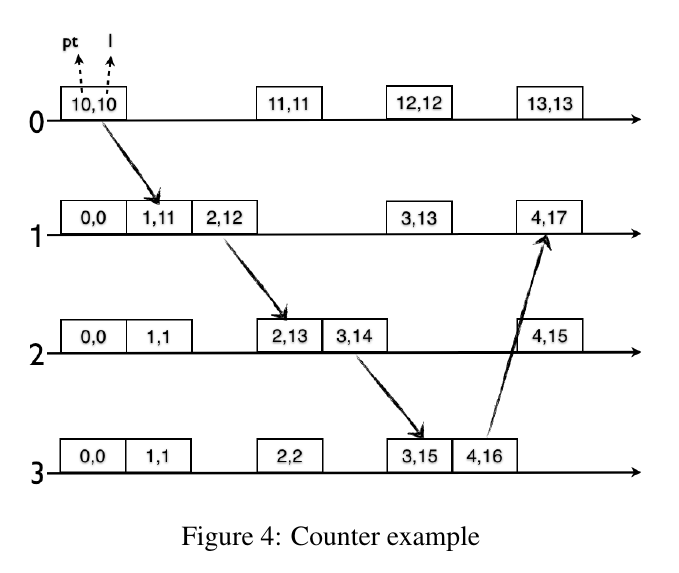
If the time for send and receive events is long enough that the physical clock of every node is incremented by at least one, the naive implementation would work.
It would be better not to depend on assumptions on physical clock rates and event generation rates across all nodes.
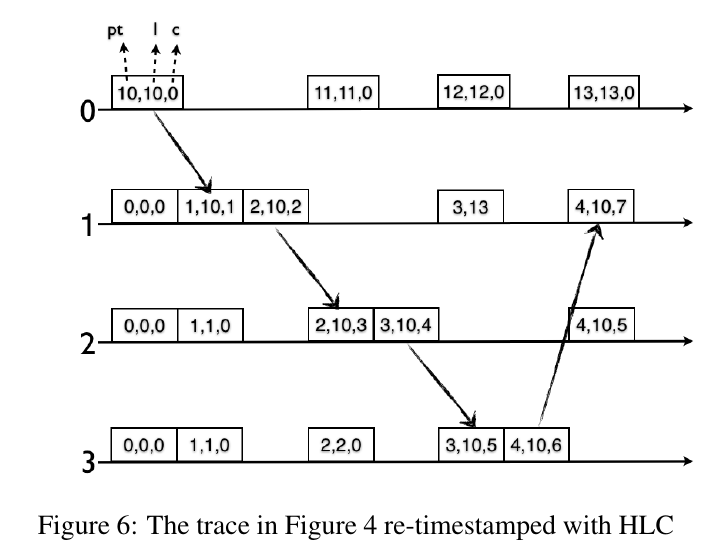
HLC
- Split \(l.j\) from naive implementation into \(l.j\) and \(c.j\)
- \(l.j\) maintains the maximum of \(pt\) learned so far
- \(c\) is used for capturing causality updates when \(l\) values are equal

Within a bounded time, one of the following is guaranteed to occur:
- Node \(j\) receives a message with a larger \(l\), \(l.j\) is updated and \(c.j\) is reset
- If node \(j\) does not hear from other nodes, \(l.j\) stays the same, and \(pt.j\) will catch up and update \(l.j\), and reset \(c.j\)
Hybrid Logical Clocks — Problem Statement
Given a distributed system, assign each event \(e\) a timestamp \(l.e\) such that:
- \(e\) "happened before" (aka \(hb\)) \(f \implies l.e \lt l.f\) ✔
- \(l.e\) can be represented with \(O(1)\) integers ✔
- \(l.e\) is represented with bounded space
- \(l.e\) is "close to" \(pt.e\), i.e. \(|l.e - pt.e|\) is bounded
Theorem 3
\(l.f\) denotes the maximum clock value that \(f\) is
aware of. In other words,
\(l.f \gt pt.f \implies (\exists g : g\; hb\; f \land pt.g = l.f)\)
Theorem 3 — proof
-
If \(f\) is a send event and \(e\) is the previous event,
then by induction, \[l.e \gt pt.e \implies (\exists g : g\; hb\; e \land pt.g = l.e)\] From the HLC algorithm, \[l.f \gt pt.f \implies l.f = pt.e\] Also, \(e\; hb\; f\), so \[l.f \gt pt.f \implies (\exists g : g\; hb\; f \land pt.g = l.f)\]
Theorem 3 — proof (cont'd)
- If \(f\) is a receive event, \(e\) is the previous event on the same node and \(m\) is the received message, \[l.f \gt pt.f \implies (l.f = l.e) \lor (l.f = l.m)\] The analysis of each of these cases is similar to the previous case. \(\;\;\square\)
Corollary 1
\(l.f\) is "close to" \(pt.f\)
i.e. \(|l.f - pt.f| \le \epsilon\)
Corollary 1 — proof
Proof: Due to clock synchronization constraints, we cannot have two events \(e\) and \(f\) such that \(e\; hb\; f\) and \(pt.e \gt pt.f + \epsilon\)
Theorem 4
For any event \(f\), \begin{align} (c.f = & k) \land (k \gt 0) \implies\\ & (\exists g_1 , g_2 , \cdots , g_k : \\ & (\forall i : 1 \le i \lt k : g_i \; hb\; g_{i + 1}) \\ & \land (\forall j : 1 \le j \lt k : l.(g_{i}) = l.f) \\ & \land g_k \; hb\; f) \end{align}
Theorem 4 — proof
In the creation of a send event, \(c.f\) is set to \(c.e + 1\) iff \(l.e = l.f\).
By induction, there exists a sequence of length \(c.e\) that satisfies the theorem statement. Also, since \(e \;hb\; f\) and \(\neg (e \;hb\; e)\), there exists a sequence of length \(c.e + 1 = c.f\) that satisfies the theorem statement. \(\;\;\square\)
From theorem 4, two corollaries follow.
Corollary 2
For any event \(f\), \[c.f \le |\{g : l.g = l.f \land g \;hb\; f \}|\;\;\square\]
Corollary 3
For any event \(f\), \[c.f \le N \ast (\epsilon + 1)\]
Corollary 3 — proof
- From Corollary 2, \[c.f \le |\{g : g \;hb\; f \land l.g = l.f\}|\]
- \(l.g \ge pt.g\)
- By clock synchronization assumption, \[pt.g \le pt.f + \epsilon\]
Corollary 3 — proof (cont'd)
The only events that can be in \(\{g : g \;hb\; f \land l.g = l.f\}\) are those that were created when the physical time of the node that created them was between \([l.f, l.f + \epsilon]\)
Since the physical clock of a node must incremented by at least 1 between any two events on that node, there are at most \(\epsilon + 1\) such events on any one node. \(\;\;\square\)
The authors make a reasonable assumption can further reduce the bound on (and size of) \(c\).
Assumption: The time for message transmission is long enough such that the physical clock of every node is incremented by at least some given parameter \(d\).
Corollary 4
\(c.f \le \epsilon / d + 1\)
Corollary 4 — proof
Suppose \(c.f = k\), \(k \gt 0\) at node \(j\)
- Theorem 4: \(\exists g_1 \cdots g_k : l.(g_1..k) = l.f\)
- Let \(p\) denote the node where \(g_1\) was created. When \(g_1\) was created, \(pt.p \le l.f\)
- Let \(q\) denote the node where \(f\) was created
- Worst case: \(q\) learned of \(g_1..k\) events from individual messages from \(p\).
- Assuming clock synchronization, when \(f\) is created \(pt.p \ge l.f + (k - 1) \ast d\)
- Under clock synchronization constraints, \(l.f + (k - 1) \ast d \le pt.f + \epsilon\)
\begin{align} l.f + (k - 1) \ast d &\le pt.f + \epsilon \\ (k - 1) \ast d &\le \epsilon + (pt.f - l.f) \\ (k - 1) \ast d &\le \epsilon \\ c.f &\le \epsilon / d + 1 \;\;\square \end{align}
For \(d \ge 1\), the naive algorithm would satisfy HLC requirements. HLC proves its size bounds by other means, but uses this corollary to reduce the bound further.
Hybrid Logical Clocks — Problem Statement
Given a distributed system, assign each event \(e\) a timestamp \(l.e\) such that:
- \(e\) "happened before" (aka \(hb\)) \(f \implies l.e \lt l.f\) ✔
- \(l.e\) can be represented with \(O(1)\) integers ✔
- \(l.e\) is represented with bounded space ✔
- \(l.e\) is "close to" \(pt.e\), i.e. \(|l.e - pt.e|\) is bounded ✔
Properties of HLC
- HLC reads the physical clock, but doesn't update it, which is nice
- Not perfect; authors suggest setting a
threshold on \(|l - pt|\) - Robust to stragglers — a straggler either learns new/higher \(l\) values by communicating, or increments \(c\)
- Robust to rushers — a rusher will set the \(l\) value for the whole system, and \(c\) will be incremented until \(pt\) catches up
Does it work in practice?
Yes. Better than expected
Empirical evaluation on AWS
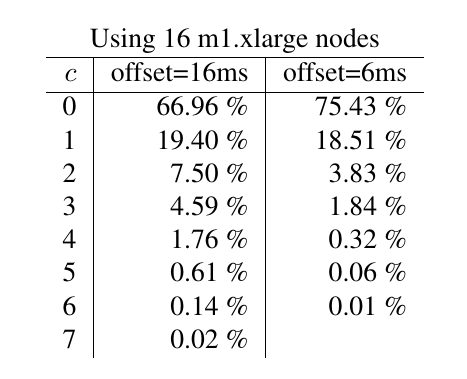
Empirical evaluation
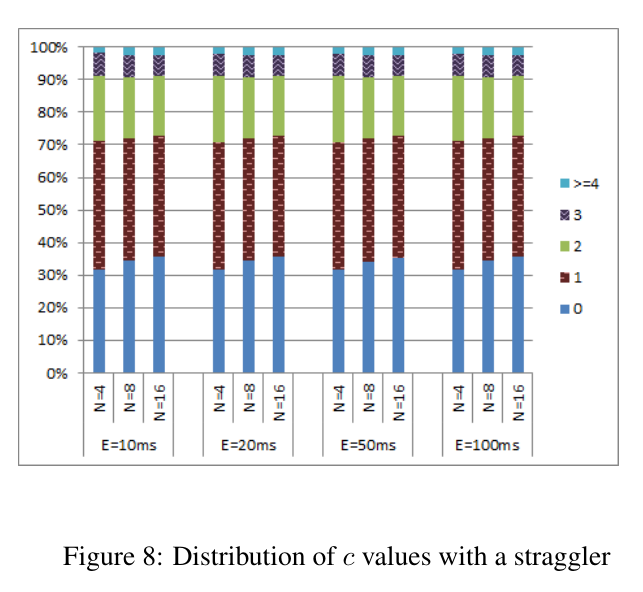
Max observed \(c = 514\)
So it keeps time pretty well.
What about snapshotting?
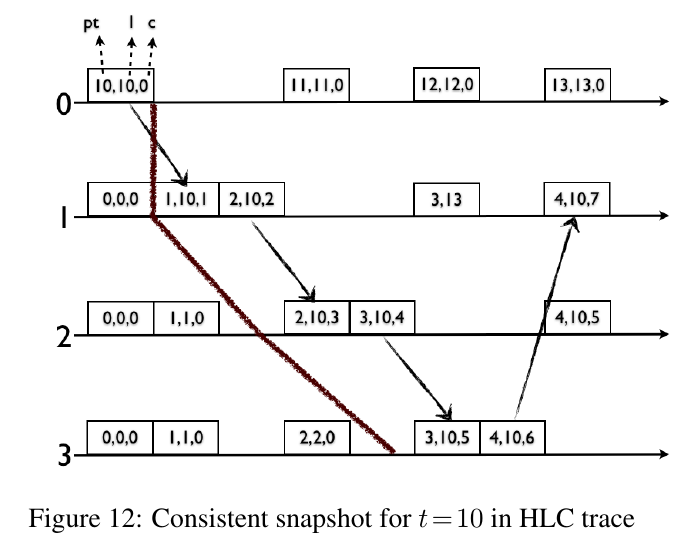
Snapshot reads
- Let \(e\) and \(f\) be two events on the same node such that \(l.e \lt l.f\)
- We introduce internal events where \(l \in [l.e + 1, l.f] \land c.f = 0\)
- Adding these events does not change timestamps of other events in the system
- For any time \(t\), there exists an event on every node where \(l = t \land c = 0\)
- The set of events on each node at time \(t\) produce a consistent global snapshot
Snapshot reads
Bit representation
- NTP uses 64-bit timestamps consisting of 32-bits for seconds and 32-bits for fraction of a second
- Using a 64-bit timestamp for HLC would be nice for compatibility with NTP
Bit representation
- \(l\) tracks the 48 most significant bits of \(pt\), and the least significant 16 bits become \(c\)
- This costs some timestamping precision, but you probably won't miss it
- When reading \(pt\) or picking query time \(t\),
round to the 48th bit - Experiments showed that 65536 values for \(c\)
is more than enough
HLC in the wild - CockroachDB
- package hlc
- Blog post: Living without atomic clocks
- int64 for \(pt\), int32 for \(c\). Optional protobuf fields
- Struct with callback for getting \(pt\)
- Goroutine that checks for large jumps
HLC in the wild - MongoDB
- logical_clock.h
- timestamp.h
- Not called HLC. Namedropped in a blog post
- Concept of "clusterTime"
- class Timestamp: fields for secs and 'i'
HLC in the wild - Yugabyte
- hybrid_time.h
- hybrid_clock.cc
- Interesting: Configurable bitmask size for \(c\)
HLC in the wild - Couchbase
Conclusion
- HLC combines the benefits of logical clocks and physical time while overcoming their individual shortcomings
- HLC has a simple algorithm and representation, making it straightforward to implement
- HLC has been shown to be more resilient in practice than in theory (!!!)
Conclusion
If you find yourself needing to track causality between events in a distributed system, consider using HLC!